It was not, however, the loss of phase that was in question. That would have decreased the values of the equatorial diameter instead of increasing them, and, what is more immediately to the point, the correction for it had already been made. This correction is easily ascertained, for it depends chiefly upon the position of the planet in its orbit, which is known with great accuracy. The resulting values, therefore, had nothing to do with the phase correction as such, but they did, nevertheless, have to do with the phase itself.



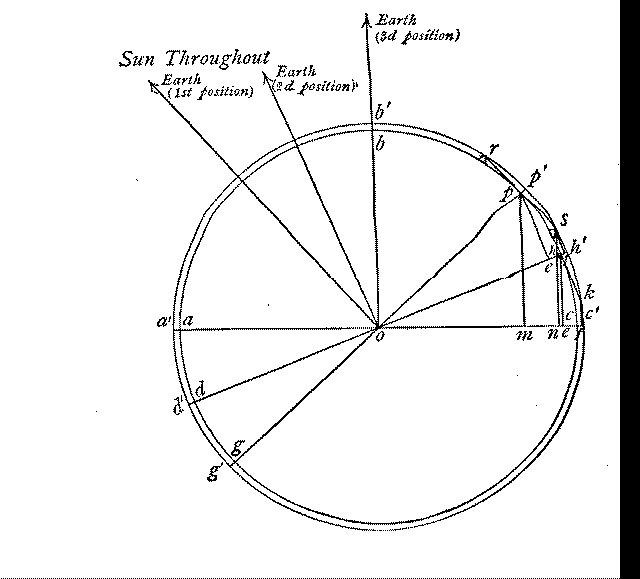
To see exactly how this is possible, let us consider the effect an illuminated atmosphere would have upon the measurements in question. To make matters more obvious we will introduce a diagram. The inner circle represents a section of the planet in the plane of the ecliptic; the arrows, the directions in the same plane of the Sun and Earth from the centre of the planet, in the different positions to be considered; and the outer circle, an atmosphere surrounding the planet, at the limit at which it is dense enough to reflect light.

At opposition the Earth lay very nearly in the same line from the planet as the Sun. This is shown by the left-hand arrow. The illuminated semi-circumference of the planet's surface, at that time also the semi-circumference seen from the Earth, was gabp , and gop was the equatorial diameter; g'a'b'p' and g'op' the semi-circumference and equatorial diameter, upon the supposition of an atmospheric envelope encircling the surface. As the Earth and Mars passed along their orbits, the line from Mars to the Earth shifted into its second position, the Sun remaining as before. The illuminated part of the surface of Mars continued, therefore, to be gabp ; but the portion of this illuminated surface visible from the Earth was only dbp , the part gd being invisible from the Earth, and the part ph lying in shadow. If, however, there were an atmosphere capable of reflecting light up to a height represented by the greater circle, the Sun's rays would strike the upper visible limit of this atmosphere, not at p' but at s , sr being drawn parallel to the line from o to the Sun. The measured equatorial diameter, which is, of course, the projection of the arc d'b's on the line d'h' , would be d'f instead of de , which it would be were there no atmosphere. It thus appears that owing to side-lengthening, as we may perhaps style this reverse of foreshortening, the fringe of atmosphere increases in apparent width with increase of phase, to an apparent increase of the equatorial diameter.

If, now, we take a third position for the Earth where Mars shows a yet greater phase, the third arrow, we find that in this case the resulting apparent increase in the equatorial diameter is mn , and we notice that mn is greater than, ef , just as ef was greater than pp' or cc'. That is, we see that the apparent increase in the size of the equatorial diameter varies directly, according to some law, with the increase in phase, or, as it is technically put, is a function of the phase.

This increase, being an increase in the measure itself, would in due course come in for its share of all the corrections applied to the diameter. In consequence, that diameter, instead of coming out simply the full equatorial diameter, would come out too big in proportion to the amount added by the twilight arc.

Pursuant, therefore, to the supposition that such was the cause of the increase, I took the means of the polar and of the equatorial diameters with regard to the time from opposition, at which the measures were made, to find myself confronted by a series of values counterparting what we have just seen would be given by the presence of a visible twilight arc. The resulting values are: --

Polar Diameters:      
     

• October 15 to 23 inc. 9".35
• October 12 and 24 to 30 inc. 9".35
• November 2 to 21 inc. 9".36

Equatorial Diameters:

• October 15 to 23 inc. 9".40
• October 12 and 24 to 30 inc. 9".43